OGATA:
INGENIERÍA DE CONTROL MODERNA, 3a. Ed.
INSTITUTO TECNOLÓGICO DE ACAPULCO
 DEPARTAMENTO
DE METALMECÁNICA
DEPARTAMENTO
DE METALMECÁNICA
INGENIERÍA
ELECTROMECÁNICA
MATERIA: Ingeniería de Control
HORARIO:
11:00 – 12:00
Capitulo
1 Introducción a los sistemas de control
RETICULA 2010
NOMBRE
DEL EQUIPO: MASTER´S
ALUMNOS:
REPRESENTANTE
DE EQUIPO:
ÁLVAREZ MILLÁN JOSÉ ÁNGEL 10320066
HUERTA
CRUZ JOSE ANTONIO 10320083
AGATON
VAZQUEZ JAVIER 10320064
APARICIO
JIMENEZ WILLIAN IVAN 10320067
Capitulo
1 Introducción a los sistemas de control
l-l Introducción
1-2 Ejemplos de sistemas de control
1-3 Control en
lazo cerrado en comparación con el control en lazo abierto 6
1-4 Diseño de
los sistemas de control
1-5 Panorama del libro
Ejemplo
de problemas y soluciones
Problemas ll
El
control automático ha desempeñado una función vital en el avance de la ingeniería
y la ciencia. Además de su extrema importancia en los sistemas de vehículos
espaciales, de guiado de misiles, robóticos y similares; el control automático
se ha vuelto una parte importante e integral de los procesos modernos
industriales y de manufactura. Por ejemplo, el control automático es esencial
en el control numérico de las máquinas-herramienta de las industrias de
manufactura, en el diseño de sistemas de pilotos automáticos en la industria aeroespacial,
y en el diseño de automóviles y camiones en la industria automotriz. También es
esencial en las operaciones industriales como el control de presión,
temperatura, humedad, viscosidad y flujo en las industrias de proceso.
Debido
a que los avances en la teoría y la práctica del control automático aportan los
medios para obtener un desempeño óptimo de los sistemas dinámicos, mejorar la
productividad, aligerar la carga de muchas operaciones manuales repetitivas y
rutinarias, así como de otras actividades, casi todos los ingenieros y
científicos deben tener un buen conocimiento de este campo.
Panorama histórico. El primer trabajo significativo en control automático fue
el regulador de velocidad centrífugo de James Watt para el control de la
velocidad de una máquina de vapor, en el siglo XVIII. Minorsky, Hazen y Nyquist, entre muchos otros, aportaron
trabajos importantes en las etapas iníciales del desarrollo de la teoría de
control. En 1922, Minorsky trabajó en los controladores automáticos para
dirigir embarcaciones, y mostr6 que la estabilidad puede determinarse a partir
de las ecuaciones diferenciales que describen el sistema. En 1932, Nyquist
diseñó un procedimiento relativamente simple para determinar la estabilidad de
sistemas en lazo cerrado, con base en la respuesta en lazo abierto en estado 1 estable cuando la entrada aplicada
es una senoidal. En 1934, Hazen, quien introdujo el término servomecanismos
para los sistemas de control de posición, analizó el diseño de los
servomecanismos con relevadores, capaces de seguir con precisión una entrada
cambiante.
Durante la década de
los cuarenta, los métodos de la respuesta en frecuencia hicieron posible que
los ‘ingenieros diseñaran sistemas de control lineales en lazo cerrado que cumplieran
con los requerimientos de desempeño. A finales de los años cuarenta y
principios de los cincuenta, se desarrolló por completo el método del lugar
geométrico de las raíces propuesto por Evans.
Los métodos de respuesta en frecuencia y del
lugar geométrico de las raíces, que forman el núcleo de la teoría de control
clásica, conducen a sistemas estables que satisfacen un conjunto más o menos
arbitrario de requerimientos de desempeño. En general, estos sistemas son
aceptables pero no óptimos en forma significativa. Desde el final de la década de
los cincuenta, el énfasis en los problemas de diseño de control se ha movido
del diseño de uno de muchos sistemas que trabajen apropiadamente al diseño de
un sistema óptimo de algún modo significativo.
Conforme las plantas modernas con muchas
entradas y salidas se vuelven más y más complejas, la descripción de un sistema
de control moderno requiere de una gran cantidad de ecuaciones. La teoría del
control clásica, que trata de los sistemas con una entrada y una salida, pierde
su solidez ante sistemas con entradas y salidas múltiples Desde alrededor de
1960, debido a que la disponibilidad de las computadoras digitales hizo posible
el análisis en el dominio del tiempo de sistemas complejos, la teoría de
control moderna, basada en el análisis en el dominio del tiempo y la síntesis a
partir de variables de estados, se ha desarrollado para enfrentar la creciente
complejidad de las plantas modernas y los requerimientos limitativos respecto
de la precisión, el peso y el costo en aplicaciones militares, espaciales e
industriales.
Durante los años comprendidos entre 1960 y
1980, se investigaron a fondo el control optimo tanto de sistemas determinativos
como estocásticos, y el control adaptable, mediante el aprendizaje de sistemas
complejos. De 1980 a la fecha, los descubrimientos en la teoría de control
moderna se centraron en el control robusto, el control de H, y temas asociados.
Ahora que las computadoras digitales se han
vuelto más baratas y más compactas, se usan como parte integral de los sistemas
de control. Las aplicaciones recientes de la teoría de control moderna incluyen
sistemas ajenos a la ingeniería, como los biológicos, biomédicos, económicos y
socioeconómicos.
Definiciones.
Variable
controlada y variable manipulada
La variable controlada
es la cantidad o condición que se mide y controla. La, variable manipulada es la cantidad o
condición que el controlador modifica para afectar el valor de la variable
controlada. Por lo común, la variable controlada es la salida (el resultado)
del sistema. Controlar significa
medir el valor de la variable controlada del sistema y aplicar la variable
manipulada al sistema para corregir o limitar una desviación del valor medido a
partir de un valor deseado.
En el estudio de la ingeniería de control, necesitamos
definir términos adicionales que resultan necesarios para describir los
sistemas de control.
Plantas.
Una
planta puede ser una parte de un equipo, tal vez un conjunto de las partes de
una máquina que funcionan juntas, el propósito de la cual es ejecutar una
operación particular. En este libro, llamaremos planta a cualquier objeto
físico que se va a controlar (tal como un dispositivo mecánico, un horno de
calefacción, un reactor químico o una nave espacial).
Procesos.
El Diccionario
Merriam-Webster define un proceso como una operación o un
desarrollo natural progresivamente continuo, marcado por una serie de cambios
graduales que se suceden uno al otro en una forma relativamente fija y que
conducen a un resultado o propósito determinados; o una operación artificial o
voluntaria progresiva que consiste en una serie de acciones o movimientos controlados,
sistemáticamente dirigidos hacia un resultado o propósito determinados. En este
libro llamaremos proceso a cualquier operación que se va a
controlar. Algunos ejemplos son los procesos químicos, económicos y biológicos.
Sistemas.
Un sistema es una combinación de componentes que actúan
juntos y realizan un objetivo determinado. Un sistema no necesariamente es
físico. El concepto de sistema se aplica a fenómenos abstractos y dinámicos,
tales como los que se encuentran en la economía. Por tanto, la palabra sistema
debe interpretarse como una implicación de sistemas físicos, biológicos,
económicos y similares.
Perturbaciones.
Una perturbación es una señal que tiende a afectar
negativamente el valor de la salida de un sistema. Si la
perturbación se genera dentro del sistema se denomina interna, en tanto que una
perturbación externa se
produce fuera del sistema y es una entrada.
Control realimentado.
El control realimentado se refiere a una operación que,
en presencia de perturbaciones, tiende a reducir la diferencia entre la salida
de un sistema y alguna entrada de referencia y lo continúa haciendo con base en
esta diferencia. Aquí ~610 se especifican con este término las perturbaciones
impredecibles, dado que las perturbaciones predecibles o conocidas siempre
pueden compensarse dentro del sistema.
1-2 EJEMPLOS
DE SISTEMAS DE CONTROL
En
esta sección presentaremos varios ejemplos de sistemas de control.
Sistema de control de velocidad. El
principio básico del regulador de velocidad de Watt para una máquina se ilustra
en el diagrama esquemático de la figura l-l.
La cantidad de combustible que se admite para la máquina
se ajusta de acuerdo con la diferencia entre la velocidad de la máquina que se
pretende y la velocidad real.
La secuencia de acciones puede describirse del modo
siguiente: el regulador de velocidad se ajusta de modo que, a la velocidad
deseada, no fluya aceite a presión en ningún lado del cilindro de potencia. Si
la velocidad real cae abajo del valor deseado debido a una perturbación,
la disminución de la fuerza centrífuga del regulador de
velocidad provoca que la válvula de control se mueva hacia abajo, aportando más
combustible y la velocidad del motor aumenta hasta alcanzar el valor deseado.
En cambio, si la velocidad del motor aumenta sobre el valor deseado, el
incremento en la fuerza centrífuga del controlador provoca que la válvula de
control se mueva hacia arriba. Esto disminuye la provisión de combustible y la velocidad
del motor se reduce hasta alcanzar el valor deseado.
En-este sistema de control de velocidad, la planta (el
sistema controlado) es la máquina y la variable controlada es la velocidad de
la misma. La diferencia entre la velocidad deseada y la velocidad real es la
señal de error. La señal de control (la cantidad de combustible) que se va a
aplicar a la planta (la máquina) es la señal de actuación. La entrada externa
que se aplica para afectar la variable controlada es la perturbación. Un cambio
inesperado en la carga es una perturbación.
Sistema de control de un robot.
Los robots industriales se usan con frecuencia en la
industria para mejorar la productividad. Un robot puede realizar tareas monótonas
y complejas sin errores en la operación. Asimismo, puede trabajar en un
ambiente intolerable para operadores humanos. Por ejemplo, puede funcionar en
temperaturas extremas (tanto altas como bajas), en un ambiente de presión alta
o baja, bajo el agua o en el espacio. Hay robots especiales para la extinción
de incendios, las exploraciones submarinas y espaciales, entre muchos otros
El robot industrial debe manejar partes mecánicas que
tengan una forma y un peso determinados.
Por tanto, debe tener al menos un brazo, una muñeca y una
mano. Debe tener la fuerza suficiente para realizar la tarea y la capacidad
para al menos una movilidad limitada.
De hecho, algunos robots actuales son capaces de moverse
libremente por sí mismos en un espacio limitado en una fábrica.
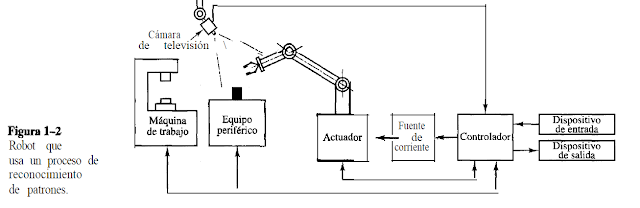
El robot industrial debe tener algunos dispositivos
sensores. A los robots de nivel bajo, se les instalan micro interruptores en
los brazos como dispositivos sensores. El robot toca primero un objeto y después,
mediante los micro interruptores, confirma la existencia de objeto en el
espacio y avanza al paso siguiente para asirlo, En un robot de nivel alto se
usa un medio óptico (como un sistema de televisión) para rastrear el fondo del
objeto. El robot reconoce el patrón y determina la presencia y orientación del
objeto. Se requiere de una computadora para procesar las señales del proceso de
reconocimiento de patrones (véase figura 1-2). En algunas aplicaciones, el
robot computarizado reconoce la presencia y orientación de cada parte mecánica
mediante un proceso de reconocimiento de patrones que consiste en la lectura de
los, números de código que se fijan a cada parte. A continuación, el robot
levanta la parte y la mueve a un lugar conveniente para su ensamble, y después
ensambla varias partes para formar un componente.
Una computadora digital bien programada funciona como
controlador.
Sistema de control de temperatura.
La figura 1-3 muestra un diagrama esquemático del control
de temperatura de un horno eléctrico. La temperatura del horno eléctrico se
mide mediante un termómetro, que es un dispositivo analógico. La temperatura analógica
se convierte a una temperatura digital mediante un convertidor A/D. La
temperatura digital se introduce a un controlador mediante una interface. Esta
temperatura digital se compara con una temperatura que se ingresa mediante un programa y si hay
una discrepancia (error) el
controlador envía una señal al calefactor, a través de una interface, un amplificador
y un relevador, para hacer que la temperatura del horno adquiera el valor
deseado.
Control de temperatura del compartimiento del
pasajero de un automóvil.
La figura 1-4 muestra un diagrama funcional del control
de temperatura del compartimiento del pasajero de un automóvil. La temperatura
deseada, convertida a, un voltaje, es la entrada del controlador. La
temperatura real del compartimiento del pasajero se convierte a un voltaje mediante
un sensor y se alimenta al controlador para que éste la compare con la entrada.
La temperatura ambiente y la transferencia térmica por, radiación del Sol, que
no son constantes conforme se conduce el automóvil, funciona como
perturbaciones. Este sistema emplea tanto un control realimentado como uno de
prealimentación. (El control prealimentado establece una acción correctiva
antes de que las perturbaciones afecten el resultado.)
La
temperatura del compartimiento del pasajero de un automóvil difiere
considerablemente dependiendo del lugar en donde se mida. En lugar de usar
sensores múltiples para medir la temperatura y promediar los valores, es
económico instalar un pequeño ventilador de succión en el lugar en donde los
pasajeros normalmente detectan la temperatura. La temperatura del aire del
aspirador es una indicación de la temperatura del compartimiento del pasajero y
se considera la salida del sistema.
El
controlador recibe la señal de entrada, la señal de salida y las señales de los
sensores de las fuentes de perturbación. El controlador envfa una señal de
control óptima al aire acondicionado o al calefactor para controlar la cantidad
de aire frío o caliente a fin de que la temperatura del compartimiento del
pasajero se mantenga al valor deseado.
Sistemas
empresariales.
Un
sistema empresarial está formado por muchos grupos. Cada tarea asignada a un
grupo representará un elemento dinámico del sistema. Para la correcta operación
de tal sistema deben establecerse métodos de realimentación para reportar los
logros de cada grupo. El acoplamiento cruzado entre los grupos funcionales debe
reducirse a un mínimo para evitar retardos de tiempo inconvenientes en el
sistema. Entre más pequeño sea dicho acoplamiento, más regular será el flujo de
señales y materiales de trabajo.
Un
sistema empresarial es un sistema en lazo cerrado. Un buen diseño del mismo reducirá
el control administrativo requerido. Observe que las perturbaciones en este
sistema son la falta de personal o de materiales, la interrupción de las comunicaciones,
los errores humanos, etcétera.
El
establecimiento de un sistema bien fundado para obtener estimados, basado en
estadísticas, es imprescindible para una administración adecuada. (Observe que
es un hecho bien conocido que el desempeño de tal sistema mejora mediante el
tiempo de previsión o anticipación.)
Con
el propósito de aplicar la teoría de control para mejorar el desempeño de tal
sistema, debemos representar la característica dinámica de los grupos
componentes del sistema mediante un conjunto de ecuaciones relativamente
simples.
Aunque
es ciertamente una dificultad obtener representaciones matemáticas de los grupos
de componentes, la aplicación de técnicas de optimización a los sistemas
empresariales mejora significativamente el desempeño de tales sistemas.
1-3 CONTROL
EN LAZO CERRADO EN COMPARACIÓN CON EL CONTROL EN LAZO ABIERTO.
Sistemas de control
realimentados.
Un sistema que
mantiene una relación prescrita entre la salida y la entrada de referencia,
comparándolas y usando la diferencia como medio de control, se denomina sistema de control realimentado. Un
ejemplo sería el sistema de control de temperatura de una habitación. Midiendo
la temperatura real y comparándola con la temperatura de referencia (la
temperatura deseada), el termostato activa o desactiva el equipo de calefacción
o de enfriamiento para asegurar que la temperatura de la habitación se conserve
en un nivel cómodo sin considerar las condiciones externas.
Los sistemas de
control realimentados no se limitan a la ingeniería, sino que también se encuentran en diversos campos ajenos a ella.
Por ejemplo, el cuerpo humano es un sistema de control realimentado muy
avanzado. Tanto la temperatura corporal como la presión sanguínea se conservan
constantes mediante una realimentación fisiológica. De hecho, la realimentación
realiza una función vital: vuelve el cuerpo humano relativamente insensible a
las perturbaciones externas, por lo cual lo habilita para funcionar en forma
adecuada en un ambiente cambiante.
Sistemas
de control en lazo cerrado.
Los sistemas de
control realimentados se denominan también sistemas de control en lazo cerrado. En la práctica,
los términos control realimentado y control en lazo cerrado se usan
indistintamente. En un sistema de control en lazo cerrado, se alimenta al
controlador la señal de error de actuación, que es la diferencia entre la señal
de entrada y la señal de realimentación (que puede ser la señal de salida misma
o una función de la señal de salida y sus derivadas y/o integrales), a fin de
reducir el error y llevar la salida del sistema a un valor conveniente. El
término control en lazo cerrado siempre implica el uso de una acción de control
realimentado para reducir el error del sistema.
Sistemas
de control en lazo abierto.
Los sistemas en los
cuales la salida no afecta la acción de control se denominan sistemas de control en lazo abierto. En
otras palabras, en un sistema de control en lazo abierto no se mide la salida
ni se realimenta para compararla con la entrada. Un ejemplo práctico es una
lavadora. El remojo, el lavado y el enjuague en la lavadora operan con una base
de tiempo. La máquina no mide la señal de salida, que es la limpieza de la
ropa.
En cualquier sistema
de control en lazo abierto, la salida no se compara con la entrada de
referencia. Por tanto, a cada entrada de referencia le corresponde una
condición operativa fija; como resultado, la precisión del sistema depende de
la calibración. Ante la presencia de perturbaciones, un sistema de control en
lazo abierto no realiza la tarea deseada.
En la práctica, el
control en lazo abierto sólo se usa si se conoce la relación entre la entrada y
la salida y si no hay perturbaciones internas ni externas. Es evidente que
estos sistemas no son de control realimentado. Observe que cualquier sistema de
control que opere con una base de tiempo es en lazo abierto. Por ejemplo, el
control del tránsito mediante señales operadas con una base de tiempo es otro
ejemplo de control en lazo abierto.
Sistemas
de control en lazo cerrado en comparación con los sistemas en lazo abierto.
Una ventaja del
sistema de control en lazo cerrado es que el uso de la realimentación vuelve
la respuesta del sistema relativamente insensible a las perturbaciones externas
y a las variaciones internas en los parámetros del sistema. Por tanto, es
posible usar componentes relativamente precisos y baratos para obtener
el control adecuado de una planta determinada, en tanto que hacer eso es
imposible en el caso de un sistema en lazo abierto.
Desde el punto de
vista de la estabilidad, el sistema de control en lazo abierto es más fácil de
desarrollar, porque la estabilidad del sistema no es un problema importante.
Por otra parte, la estabilidad es una función principal en el sistema de
control en lazo cerrado, lo cual puede conducir a corregir en exceso errores
que producen oscilaciones de amplitud constante o cambiante.
Debe
señalarse que, para los sistemas en los que se conocen con anticipación las
entradas y en los cuales no hay perturbaciones, es aconsejable emplear un
control en lazo abierto. Los sistemas de control en lazo cerrado sólo tienen
ventajas cuando se presentan perturbaciones impredecibles y/o variaciones
impredecibles en los componentes del sistema.
Observe
que la valoración de la energía de salida determina en forma parcial el costo,
el peso y el tamaño de un sistema de control. La cantidad de componentes usados
en un sistema de control en lazo cerrado es mayor que la que se emplea para un
sistema de control equivalente en lazo abierto. Por tanto, el sistema de
control en lazo cerrado suele tener costos y potencias más grandes. Para
disminuir la energía requerida de un sistema, se emplea un control en lazo
abierto cuando puede aplicarse. Por lo general, una combinación adecuada de
controles en lazo abierto y en lazo cerrado es menos costosa y ofrecerá un
desempeño satisfactorio del sistema general.
1-4 DISEÑO DE LOS SISTEMAS
DE CONTROL
Los sistemas de control actuales son, por lo
general, no lineales. Sin embargo, si es posible aproximarlos mediante modelos
matemáticos lineales, podemos usar uno o más métodos de diseño bien
desarrollados. En un sentido práctico, las especificaciones de desempeño determinadas
para el sistema particular sugieren cuál método usar. Si se presentan las
especificaciones de desempeño en términos de las características de respuesta
transitoria y/o las medidas de desempeño en el dominio de la frecuencia, no
tenemos otra opción que usar un enfoque convencional basado en los métodos del
lugar geométrico de las raíces y/o la respuesta en frecuencia. (Estos métodos
se presentan en los capítulos 6 al 9.) Si las especificaciones de desempeño se
presentan como índices de desempeño en términos de las variables de estado,
deben usarse los enfoques de control moderno. (Estos enfoques se presentan en
los capítulos ll al 13.)
En tanto que el diseño de un sistema de
control mediante los enfoques del lugar geométrico de las raíces y de la
respuesta en frecuencia es una tarea de la ingeniería, el diseño del sistema en
el contexto de la teoría de control moderna (métodos en el espacio de estados)
emplea formulaciones matemáticas del problema y aplica la teoría matemática para
diseñar los problemas en los que el sistema puede tener entradas y salidas
múltiples y ser variantes con el tiempo. Aplicando la teoría de control
moderna, el diseñador puede iniciar a partir de un índice de desempeño, junto
con las restricciones impuestas en el sistema, y avanzar para diseñar un
sistema estable mediante un procedimiento completamente analítico. La ventaja
del diseño basado en la teoría de control moderna es que permite al diseñador
producir un sistema de control óptimo en relación con el índice de desempeño considerado.
Los sistemas que pueden diseñarse mediante un
enfoque convencional están por lo general limitados a una entrada y una salida,
y son lineales e invariantes con el tiempo. El diseñador busca satisfacer todas
las especificaciones de desempeño mediante la repetición estudiada de prueba y
error. Después de diseñar un sistema, el diseñador verifica si satisface todas
las especificaciones de desempeño. Si no las cumple, repite el proceso de
diseño ajustando los parámetros o modificando la configuración del sistema
hasta que se cumplan las especificaciones determinadas. Aunque el diseño se
basa en un procedimiento de prueba y error, el ingenio y los conocimientos del
diseñador cumplen una función importante en un diseño exitoso. Un diseñador
experimentado será capaz de diseñar un sistema aceptable sin realizar muchas
pruebas.
Por lo general, es
conveniente que el sistema diseñado exhiba la menor cantidad posible de
errores, en respuesta a la señal de entrada. A este respecto, debe ser
razonable el amortiguamiento del sistema. La dinámica del sistema debe ser
relativamente insensible a variaciones pequeñas en sus parámetros. Las
perturbaciones no deseadas deben estar bien atenuadas. [En general, la parte de
alta frecuencia debe atenuarse rápido para que puedan atenuarse los ruidos de
alta frecuencia (como ruidos de los sensores). Si se conoce el ruido o las
frecuencias de perturbación, pueden usarse filtros de ranura para atenuar estas
frecuencias específicas.] Si el diseño del sistema se reduce a unos cuantos
candidatos, puede hacerse una elección óptima entre ellos a partir de consideraciones
como el desempeño general proyectado, el costo, el espacio y el peso.
1-5
PANORAMA DEL LIBRO
A continuación
presentaremos brevemente el orden y el contenido del libro.
El capítulo 1
contiene el material introductorio sobre los sistemas de control. El capítulo 2
presenta la teoría de la transformada de Laplace, necesaria para el entendimiento
de la teoría de control que se presenta en el libro. El capítulo 3 aborda el
modelado matemático de sistemas dinámicos mediante funciones de transferencia y
ecuaciones en el espacio de estados. Este capítulo incluye el análisis de alinealización
de sistemas no lineales.
El capítulo 4 trata
los análisis de respuesta transitoria de sistemas de primer y segundo orden.
Este capítulo también
proporciona detalles de los análisis de respuesta transitoria con MATLAB. El
capítulo 5 presenta, primero, las acciones básicas de control y, después,
analiza los controladores neumáticos, hidráulicos y electrónicos. Asimismo,
este capítulo se refiere al criterio de estabilidad de Routh.
El capítulo 6 aporta
un análisis del lugar geométrico de las raíces de los sistemas de control. Se
presentan las reglas generales para desarrollar los lugares geométricos de las
raíces. Se incluyen análisis detallados para grafica lugares geométricos de las
raíces con MATLAB.
El capítulo 7 aborda
el diseño de los sistemas de control mediante el método del lugar geométrico de
las raíces. Específicamente, se analizan en detalle los enfoques del lugar geométrico
de las raíces para el diseño de compensadores de adelanto, de atraso y de
adelanto- atraso. El capítulo 8 ofrece el análisis de la respuesta en
frecuencia de los sistemas de control. Se revisan las trazas de Bode, las
trazas polares, el criterio de estabilidad de Nyquist y la respuesta en
frecuencia en lazo cerrado. El capítulo 9 se dedica al diseño de sistemas de
control mediante el enfoque de la respuesta en frecuencia. Aquí se usan las
trazas de Bode para diseñar compensadores de adelanto, de atraso y de
adelanto-atraso. El capítulo
10 trata los
controles PID básicos y modificados. Los temas que se incluyen son las reglas para
sintonizar los controladores PID, las modificaciones de esquemas de control
PID, el control con dos grados de libertad y consideraciones de diseño para el
control robusto.
El capítulo ll
presenta el material básico para el análisis en el espacio de estados de sistemas
de control. Se deriva la solución de las ecuaciones de estado invariantes con
el tiempo y se analizan conceptos de controlabilidad y observabilidad. El
capítulo 12 trata el diseño de sistemas de control en el espacio de estados.
Este capítulo empieza con problemas de ubicación de polos, seguidos por el
diseño de observadores de estados y concluye con el diseño de sistemas de
seguimiento de tipo 1. Se utiliza MATLAB para resolver los problemas de
ubicación de polos, el diseño de observadores de estados y el diseño de
sistemas de seguimiento. El capítulo 13, que es el último, presenta el análisis
de estabilidad de Liapunov y el control cuadrático óptimo. Este capítulo
empieza con el análisis de estabilidad de Liapunov. A continuación, se usa el
enfoque de estabilidad de Liapunov para Diseñar sistemas de control con modelo
de referencia. Por último, se analizan en detalle problemas de control
cuadrático óptimo. Aquí se emplea el enfoque de estabilidad de Liapunov para
derivar la ecuación de Riccati para un control cuadrático óptimo. Se incluyen soluciones
de MATLAB para los problemas de control cuadrático óptimo.
El apéndice resume
los fundamentos necesarios para el uso efectivo de MATLAB. Este apéndice se
presenta específicamente para aquellos lectores que todavía no están familiarizados
con MATLAB.
EJEMPLO DE PROBLEMAS
Y SOLUCIONES
A-l-l. Haga una lista
de las ventajas y desventajas principales de los sistemas de control en lazo
abierto.
Solución. Las
ventajas de los sistemas de control en lazo abierto son las siguientes:
1. Una construcción
sencilla y un mantenimiento fácil.
2. Son menos costosos
que un sistema equivalente en lazo cerrado.
3. No existe el
problema de estabilidad.
4. Son convenientes
cuando es difícil medir la salida o no son factibles en el aspecto económico.
(Por ejemplo, en el
sistema de una lavadora, sería muy costoso ofrecer un dispositivo para medir la
calidad de la salida -la limpieza de la ropa- de la lavadora.)
Las desventajas de
los sistemas de control en lazo abierto son las siguientes:
1. Las perturbaciones
y los cambios en la calibración provocan errores y la salida puede ser
diferente de lo que se busca.
2. Para conservar la
calidad requerida en la salida, es necesaria una recalibración de vez en cuando.
A-1-2. La figura
l-5(a) es un diagrama esquemático de un sistema de control de nivel de líquido.
Aquí el controlador automático mantiene el nivel de líquido comparando el nivel
real con un nivel deseado y corrigiendo cualquier error mediante un ajuste de
la apertura de la válvula neumática. La figura l-5(b) es un diagrama de bloques
del sistema de control. Dibuje el diagrama de bloques correspondiente para un
sistema de control de nivel de líquido operado por personas.
Solución. En el
sistema operado por personas, los ojos, el cerebro y los músculos corresponden al
sensor, el controlador y la válvula neumática, respectivamente. La figura 1-6
muestra un diagrama de bloques.
A-1-3. Un sistema de
ingeniería organizacional está formado por los grupos principales, como son la
administración, la investigación y el desarrollo, el diseño preliminar, los
experimentos, el diseño y boceto de los productos, la fabricación y el ensamble
y las pruebas. Estos grupos se conectan entre sí para formar la operación
completa.
Para analizar el
sistema, se reduce al conjunto de componentes más elemental, necesario para ofrecer
el detalle analítico, y se representan las características dinámicas de cada
componente mediante un grupo de ecuaciones simples. (El desempeño dinámico de
tal sistema se determina de la relación entre el logro progresivo y el tiempo.)
Dibuje un diagrama de
bloques funcional que muestre un sistema de ingeniería organizacional.
Solución. Un diagrama
de bloques funcional se dibuja mediante los bloques para representar las
actividades funcionales y conectando líneas de señales para representar la
salida de información o de productos de la operación del sistema. Un diagrama
de bloques posible se muestra en la figura 1-7.